2.4 SciPy Scientific Python¶
SciPy is a free and open-source Python library used for scientific computing and technical computing. SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and engineering. Wikipedia
We will look at three tool sets from SciPy:
(1) Curve Fitting,
(2) Solving Ordinary Differential Equations, and
(3) Minimizing Loss Functions.
Ex 2.4.1 Linear Regression¶
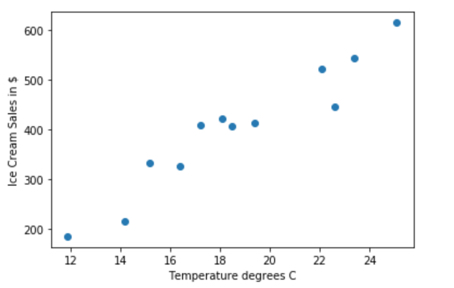In an earlier example in matplotlib we plotted this scatter data for ice cream sales vs. temperature. In this example we will fit a straight line to the data.
Lines 2-4 import libraries. NOTE: when you import a single element using from scipy.optimize import curve_fit, you can refer to this without specifying the library. When importing the entire library numpy, it is necessary to use np.
Lines 7-8 define the function to model the data. You may use any name f, my_fun,...model. Note here we will pass in an array of values for x (our data set) and return ax+b. The arguments of the function are x,a, and b.
Lines 11-12 This is the x (temperature) and y (ice cream sales) data we use to fit the data
Line 16 The x and y data arrays as well as the function name model are passed as parameters in curve_fit()
The output is a tuple param (here a and b, and the covariance). The covariance is a measure of the 'goodness' of the fit.
Line 20 This is the predicted y value using the fit model.
# Ex 2.4.1
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np
# equation to model the data
def model(x, a,b):
return a*x+b
# The data Temp in C is plotted on x axis and sales is plotted on the y axis
xdata=np.array([14.2,16.4,11.9,15.2,18.5,22.1,19.4,25.1,23.4,18.1,22.6,17.2])
ydata=np.array([215,325,185,332,406,522,412,614,544,421,445,408])
# use curve_fit to fit the data
params, covs = curve_fit(model, xdata, ydata)
print(params, covs)
yp=model(xdata,params[0],params[1])
plt.xlabel('Temperature degrees C')
plt.ylabel('Ice Cream Sales in $')
plt.scatter(xdata,ydata)
plt.plot(xdata,yp, c='red')
plt.show()
Ex 2.4.2 Fitting non-linear functions to data.¶
The following data source lists United States Census data from 1910 to 2020. We would like to fit a polynomial to this data.
data source: https://www.census.gov/data/tables/time-series/dec/popchange-data-text.html
lines 5-6 We propose to fit a quadratic function with three parameters a,b, and c to the data.
lines 7-8 The census years and reported population
line 10 Fit the quadratic equation to the data.
lines 16-20 Plot the data and the fitted curve.
# Ex 2.4.2
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np
def model(x, a,b,c):
return a+b*x+c*x**2
year=np.array([1910,1920,1930,1940,1950,1960,1970,1980,1990,2000,2010,2020])
pop=np.array([92.23,106.02,123.20,132.17,151.33,179.32,203.21,226.55,248.71,281.42,308.75,331.45])
params, covs = curve_fit(model, year, pop)
print(params, covs)
plt.scatter(year,pop)
plt.plot(year,model(year,params[0],params[1],params[2]), c='red')
plt.xlabel('year')
plt.ylabel('population')
plt.show()
Ex 2.4.3 Solving Differential Equations¶
Given the differential equation $\frac{d^2 x}{dt^2} + c_1\frac{dx}{dt}+ c_2x=0$ we can express this equation as a system of first order differential equations where the state z is a vector[z1,z2]= [x,dx/dt].
$\frac{dz_1}{dt}=z_2$
$\frac{dz_2}{dt}=-c_1z_2-c_2z_1$
We will represent this system of two first order differential equations in vector form:
dx/dt=f(x,t) where z0=$[z1(t=0),z2(t=0)]$
We will use odeint() from scipy.integrate to solve the differential equation
The required arguments for odeint(f,ic,t,...options) where
(1) f is the name of the function defined as the right hand side of the differential equation.
(2) ic is the initial condition of the state variables (tuple)
(3) t A sequence of time points (can be defined by np.linspace()
The odeint function returns an array containing the value of y for each desired time in t, with the initial value y0 in the first row.
odeint documentation
Lines 4-6 import critical libraries. Here we will use odeint from scipy.integrate.
Lines 9-12 This is the definition of the right hand side of the system of first order equations we are solving. Here sv is an array with two elements--the state variables x=sv[0] the position and sv[1] the velocity. line 10 assigns x to the first element of sv, and v to the second element of sv. We could alternately replace this by two equations x=sv[0] and v=sv[1] We are returning dx/dt. $dx/dt=x_1$ and $dv/dt=-c_1v-c_2x$ . These are the two components in an array [...,...],
Line 15 gives the initial state: initial displacement=1, and initial velocity=0.
Line 18 establishes the initial conditions of the state vector sv0 as a tuple. x(0)=1 and v(0)=0.
line 21 creates the time sequence using np.linspace(). This time sequence t will be passed as an argument to odeint()
Lines 24 Since the function odeint returns an array of values of the state variables sv for each time in t, we will assign sv=odeint().We index sv using either 0 or 1 for the position or velocity lines 22-23 What is the colon in these statements? Actually the solution is a two dimensional array 2x100. Where 2 is the dimension of the state vector and 100 is the number of data points. To return an array of all values of x we index solution[:,0] Meaning all values of time. this is a 1x100 array which we can plot.
Lines 26-40 We have already done this kind of plotting using axis twins when we introduced matplotlib. This allows us to share a time axis, but have separate axes for displacement and velocity.
# Ex 2.4.3
# import libraries for plotting, arrays, and numerics
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# definition of the right hand side of dx/dt=f(x,t)
def f(sv,t):
x,v =sv
c1=.2
c2=1.0
dxdt=v
dvdt=-c1*v-c2*x
return[dxdt,dvdt]
# initial conditions
sv0=(1.0,0.0)
# define time axis
t=np.linspace(0,10,100)
# integrate ODE and store result
sv=odeint(f,sv0,t)
x=sv[:,0]
v=sv[:,1]
# Creates an axes ax1 in a figure named fig
fig, ax1 = plt.subplots()
# Creates the labels for each Axis associated with ax1
ax1.set_ylabel("position")
ax1.set_xlabel("time")
# Plots the data for distance
ax1.plot(t, x, c='b', label='position')
# Creates an axes ax2 which is a twin of ax1
ax2 = ax1.twinx()
# Creates the labels for each Axis associated with ax2
ax2.set_ylabel("velocity")
ax2.plot(t, v, c='g', label='velocity')
# Set display parameters
plt.legend()
fig.set_size_inches(7,5)
plt.show()
Ex 2.4.4 Solving Nonlinear ODEs¶
There is a classic set of nonlinear differential equations which models the interaction among preditors and prey. In the following two equations x is a population of prey (e.g. mice) and y is a population of predators (coyotes). The first equation shows that the prey population would grow unchecked if it were not for the predators. The interaction of the two groups is modeled by a product of the two populations. In a similar manner, without the food source of the rodents, the population of the predators would diminish. The product of the two populations reinforces the growth of the predators population. Of course, this is a very simple model, but it does reflect the interaction of the species.
$\frac{dx}{dt}=ax-bxy$ \
$\frac{dy}{dt}=-cy+dxy$
This example follows the same structure as the harmonic oscillator in the previous example, EXCEPT in that case, we defined the parameters of the differential equation within the function f. We could do that in this example, but have chosen to pass the parameters into the function f which is called by odeint.
Lines 8-18 define the vector differential equation. Here sv is the state vector and params is a tuple holding the values of the coefficients of in the differential equation.
lines 11-13 we unpack the values of x and y from the tuple sv, and the constants a,b,c,d from the tuple params.
lines 15-18 we define our the right hand side of f(x,y) for the vector differential equation.and return the derivatives [dxdt, dydt].
Lines 21-27 We assign initial values for the state vector sv0 of x(0)=10 and y(0)=1 (these are given in hundreds of animals). We define the time sequence using np.linspace(), and assign values to a,b,c, and d which are coefficients in the differential equations. We bind these paramters into a tuple named params line 12
Line 30 solves the differential equation using odeient(). The odeint function returns an nxm array where n is the length of the time sequence and m is the dimension of the state vector. In this case 1000x2. The arguments are: the name of the function f, the initial value of the state vector sv0, the time sequence t, and the parameters we pass to odeint. Note: we cannot simply pass additional values like a=..., b=..., etc. since odeint is a DEFINED FUNCTION. Additional parameters must be passed as a tuple in the form: args=(params,). The differential equation is solved for each value of time in the time sequence.
Lines 33-34 unpack x and y from the sv array. For x we use the second index=0, while y has a second index of 1. the colon : means that we take ALL values of the first index. Thus, x and y are each 100x1 arrays.
Lines 32-55 create two plots of the solution. The first plot is the time history of the prey x(t) and the preditor y(t). Notice that as the predators increase their population, they check the growth of the prey population. As the prey population declines, the food base for the predators diminishes, and their numbers begin to decline, leading the another growth in the prey. This cyclic behavior of preditor/prey ecologies reflects natural evolution of populations. The second graph plots the prey population versus the predator population. Again we see a cycle in the state space (x,y). The cycle moves in a counter clockwise direction.
Experiment
In the main program include a for loop for different initial conditions. Note that you can find an equilibrium population for x and y by setting the time derivatives to zero. This is a stable equilibrium. Given values for a,b,c, and d, you obtain 2 equations in 2 unknowns. Solving these equations gives the equilibrium populations.$(x_e,y_e)$. Choose initial 4 or 5 sets of initial conditions between the one simulated here and the equilibrium values. Plot only the (x,y) phase portrait. You should get a series of orbits around the equilibrium point. Given that the data of these populations is accurate, how might you use this to BEST check the growth of a pest (prey) by introducing predation?
# Ex 2.4.4
# import libraries for plotting, arrays, and numerics
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# definition of the right hand side of dx/dt=f(x,t)
def f(sv, t, params):
# x is prey population and y= preditor population
x,y = sv
a,b,c,d=params
# this is equivalent to four statements a=params[0], b=params[1], c=params[2] and d=params[3]
dxdt = a*x - b*x*y
dydt = -c*y + d*x*y
return[dxdt, dydt]
# main program
sv0 = [10,1] # [prey, preditors] units in hundreds
t = np.linspace(0,50,num=1000)
a = 1.1
b = 0.4
c = 0.4
d = 0.1
params = (a,b,c,d)
# the differential equation solver.
sv = odeint(f, sv0, t, args=(params,))
# plotting the results
x=sv[:,0] #prey
y=sv[:,1] #preditor
# Creates an axes ax1 in a figure named fig
fig, ax1 = plt.subplots()
# Creates the labels for each Axis associated with ax1
ax1.set_ylabel("prey")
ax1.set_xlabel("time")
# Plots the data for distance
ax1.plot(t, x, c='b', label='prey')
# Creates an axes ax2 which is a twin of ax1
ax2 = ax1.twinx()
# Creates the labels for each Axis associated with ax2
ax2.set_ylabel("preditor")
ax2.plot(t, y, c='g', label='preditor')
# Set display parameters
plt.legend()
fig.set_size_inches(10,5)
plt.show()
plt.plot(x,y)
plt.xlabel('prey')
plt.ylabel('preditor')
plt.show()
Ex 2.4.5 Root Solving¶
Scipy has functions to solve systems of equations. The next example is a very straight forward cubic polynomial. $x^3+3x^2+2x=0$ . We will invoke this method by fsolve from scipy.optimize. The steps to invoke the method are:
- Write the function to be solved in the form f(x)=0 (it already is in this form).
- Define a function that returns the value of f(x) given x.
- After the method finds the roots, assign some variable y=fsolve(f,[-2.5,-1.0,.5]). Here we know there should be three roots and [-2.5,-1.0,.5] is a list of first guesses at the values of the roots (required).
line 9 print the solution-- note this will be a list.
lines 10-14 Plot to confirm the results. Note: the blue line is the cubic polynomial. We did a scatter plot of the roots plt.scatter(y,f(y),marker="D"). The dotted line is the y=0 plotted using lines 11-12
fsolve() documentation
Experiment
Try different initial estimates for the roots.[-3.,-1,8,,5] Notice that the solution will converge to the same root for the initial guess of -3 and -1. Reasonable estimates of the solution are important.
Change the value of K in the function f(x) to 2. Re run. What happens? Hint, this method should not be used to find the roots of equations with complex roots. We will deal with that later.
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
def f(x):
K=.2
return x**3+3.0*x**2+2.0*x+K
x= np.linspace(-2.5,0,num=1000)
y=fsolve(f,[-2.5,-1.0,.5])
print('the roots of the equation are',y)
plt.plot(x,f(x))
z=np.linspace(0,0, num=1000)
plt.plot(x,z,c='black',ls='--')
plt.scatter(y,f(y),marker="D")
plt.show()
Ex 2.4.6 Location of Webb Telescope¶
We now turn to apply the fsolve method to a real world problem. The recently launched James Webb Space Telescope was placed in orbit at the L2 Lagrange point. Lagrange points were postulated by Joseph-Louis Lagrange in 1772. In the sun-earth frame there are points in which there is a balance of gravitational forces of the sun and earth and the centrifugal forces of the orbiting body. As such, there is no net force impinging on a satellite placed at L2. Unfortunately, this is an unstable point; any small variation from the L2 location will cause the satellite to move uncontrollably from this point. However, from a practical point of view, it is possible to put a satellite in orbit around the L2 point such that there is minimal expenditure of fuel to keep the body in orbit.
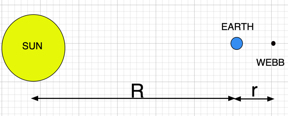If we define $x=10^{-9}r$, then the equation locating the Lagrange point is given by: $$f(x)=\frac{10.125}{x^2(150+x)}+\frac{3.375\times 10^6}{(150+x)^3}-1=0$$ .
Note on Webb Telescope and derivation of the above equation
# Ex 2.4.6
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
def f(x):
return 10.125/((x**2)*(150+x))+3.375e+06/((150+x)**3)-1
x= np.linspace(1.2,1.8,1000)
plt.plot(x,f(x))
plt.axhline(y=0.0, color='black', linestyle='--')
plt.xlabel('x=$10^{-9}r$')
plt.ylabel('f(x)')
plt.show()
y=fsolve(f,1.2)
print('x=',y,'\n y=',y*100,'million km')
Ex 2.4.7 Solving multiple equations using fsolve()¶
The method fsolve() is designed to solve non linear equations of the form f(x)=0. this also works if f and x are vectors.
Consider the simple example
$$3xy+y-z-10=0$$
$$x+x^2y+z-12=0$$
$$x-y-z=2=0$$
line 2 when you import a single method from a library, you can refer to it by its name. There is no need to write scipy.optimize.fsolve
line 5 This defines the vector function f(vars)=0 vars is a tuple whose values represent (x,y,z).
line 6 Unpacking x, y, and z from vars
lines 7-9 the vector of functions which depend on x,y,z.
line 10 return the list of values of the vector function. For the initial guess, these will not be zeros.
line 13 invoking the fsolve method on the vector function f, with an initial guess x=1,y=1,z=1 for the solution. The fsolve method examines perturbations from these initial values, and predicts a new estimate for the solution. It again calls the function, repeating the iterations until it concludes that it has found the solution.
line 17 Verifying that f1, f2, and f3 are approximately zero.
# Ex 2.4.7
from scipy.optimize import fsolve
# define the functions
def f(vars):
x, y, z = vars
f1 = 3*x*y + y - z -10
f2 = x + x**2*y + z -12
f3 = x -y -z + 2
return [f1, f2, f3]
# find the solution and print x,y, and z
x, y, z = fsolve(f, (1, 1, 1))
print('x =', x, 'y =', y, 'z =', z)
#verify that for the solution f1, f2, and f3 are (essentially) zero.
print(' f1=',3*x*y + y - z -10,'\n f2=',x + x**2*y + z -12,'\n f3=',x -y -z + 2)
Finding minima and maxima¶
Optimization is a topic that could fill an entire graduate level course by itself. In this section I will solve a few problems, but if you want to know more about the choices there are in scipy for doing optimization, here is a brief summary: https://scipy-lectures.org/advanced/mathematical_optimization/
f(x,y)=(a-x)^{2}+b(y-x^{2})^{2}
Reference Guide: scipy.optimize.minimize()
Ex 2.4.8¶
In this example we will attempt to find the minimum of the function
$$x^2+10sin(x)$$
lines 2-4 import library packages
lines7-9 define the function to be minimized. Notice we are using sine function from numpy.
line 12 this calls opt.minimize and uses an initial guess of var=-3. The mimimize method explores the function, picks a best next guess and evaluates the function again. Iteration continues until convergence to a minimum.
line 13 result carries a lot of information regarding the solution. These include: the value of the function, a message, the number of iterations, and the value of the optimum point. Rather than printing result line 12 comment that out and print result.x and result.fun; this is the way in which we refer to these compoents in result.
lines 21-24 produce a graph of the function with the solution of the minimum indicated by the diamond.
Experiment
- Start with an initial guess of 10 instead of -3. What happens? opt.minimize converges to a RELATIVE minimum. If you don't have any idea what the function looks like, it is possible to rerun this in a loop for different starting values and reject relative minima as you explore.
#Ex 2.4.8
import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt
# Define the function to minimize
def f(var):
x=var
return x**2 + 10*np.sin(x)
# Find the minimum value of the function
result = opt.minimize(f, -3)
print(result)
# Print the minimum value of the function
print('\nThe minimum is x=',result.x)
print('\nThe value of f(xmin)=',result.fun)
# Print the x-value resulting in the minimum value
x=np.linspace(-3,10,1000)
plt.plot(x,x**2 + 10*np.sin(x))
plt.scatter(result.x,result.fun,marker="D")
plt.show()
Ex 2.4.9 Finding minima in more than one dimension¶
In this example we will explore finding the minimum of a function of two variables x and y.
$$(x-.5)^2+.75xy+(y-1.0)^2$$
Lines 5-7 define the function of x and y to be minimized.
Line 10 finds the minimum Notice xmin=res.x[0] and ymin=res.x[1]
Lines 42-43 are used to locate the minimum point on the plot.
plt.axhline(y=result.x[1], color='black', linestyle='--')
plt.axvline(x=result.x[0], color='black', linestyle='--')
# Ex 2.4.9
import scipy.optimize as opt
# define function to be minimized
def f(vars):
x,y=vars
return (x-.5)**2+.75*x*y+(y-1.0)**2
# minimize the function f with the starting value x=1.5, y=-1.0
result = opt.minimize(f, (1.5,-1.0))
print(result.message,'\n')
print('xmin=',result.x[0],'\n')
print('ymin=',result.x[1],'\n')
print('the minimum value of the function=',result.fun)
# Plot a contour map for the function and verify the minimum
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
# define meshpoint in the x,y plane
x_value=np.linspace(-2, 2, 1000)
y_value=np.linspace(-2, 2, 1000)
x,y = np.meshgrid(x_value, y_value)
# define the surface to be plotted
z = (x-.5)**2+.75*x*y+(y-1.0)**2
# set up the figure and axes
fig = plt.figure(figsize=(10,10))
ax = plt.axes()
# specify plotting for a contour map
cp=ax.contour(x,y,z, cmap=cm.coolwarm, levels=[0,.25,.5,.75,1,2,4])
ax.clabel(cp, fontsize=9, inline=True)
ax.set_title('Contour plot of $(x-.5)^2+.75xy+(y-1)^2$ \n\n',fontsize=25)
plt.scatter(result.x[0],result.x[1],result.fun,marker="*")
plt.plot(result.x[0],)
plt.axhline(y=result.x[1], color='black', linestyle='--')
plt.axvline(x=result.x[0], color='black', linestyle='--')
plt.show()
Ex 2.4.10¶
The next function we will explore is the Rosenbrock function https://en.wikipedia.org/wiki/Rosenbrock_function
This has been called the banana valley function; it is a particularly difficult function to explore for a minimum as the gradients perpendicular to the valley floor are quite steep, while the floor of the valley has a very shallow slope.
$$(2-x)^2+5(y-x^2)^2$$
# Ex 2.4.10
import numpy as np
from scipy.optimize import minimize
def f(vars):
x,y=vars
return (2-x)**2+5*(y-x**2)**2
res = minimize(f, (.5,1))
print(res)
# Plot a contour map for the function and verify the minimum
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
# define meshpoint in the x,y plane
x_value=np.linspace(0, 3, 1000)
y_value=np.linspace(-2, 6, 1000)
x,y = np.meshgrid(x_value, y_value)
# define the surface to be plotted
z = (2-x)**2+5*(y-x**2)**2
# set up the figure and axes
fig = plt.figure(figsize=(10,10))
ax = plt.axes()
# specify plotting for a contour map
cp=ax.contour(x,y,z, cmap=cm.coolwarm, levels=[0,.25,.5,.75,1,2,4])
ax.clabel(cp, fontsize=9, inline=True)
ax.set_title('Contour plot of $(2-x)^2+5(y-x^2)^2$ \n\n',fontsize=25)
plt.axhline(y=res.x[1], color='black', linestyle='--')
plt.axvline(x=res.x[0], color='black', linestyle='--')
plt.show()
Ex 2.4.11 Using minimize() to Identify Parameters in a Differential Equation¶
In this problem we are not finding the minimum of a function like those found in the last two examples. Rather, we will return to the example 2.4.3 and ask if given a recording of the displacement x(t) sampled over time, can we find an appropriate set of paramters (in this case $c_1$ and $c_2$ that best fit the data? We will postulate that this is a second order differential equation with unknown coefficients $c_1$ and $c_2$. Given a sequence $x_n$ and $t_n$ can we find an the parameters to be a best fit to the response.
Lines 2-6 Import required libraries. Notice a new library csv. this allows us to access data from a comma separated file to be read into our program.
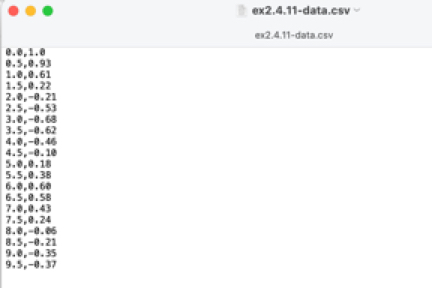
Lines 9-18 Here we read data from a file. Each row in the data file is a value for the sampled time is float(row[0]) and the sampled displacement float(row[1]) (these data are separated by commas. These values from the file are appended to the lists tt and xx. NOTE: THE csv.reader will return string data; we must change this to float (cast as float).
Lines 21-32 This fuction sim(sv,t,params) defines the differential equation. It is the same differential equation as Ex 2.4.3 EXCEPT that the coefficients $c_1$ and $c_2$ are unknown and passed to sim in the params. Lines 23-27 unpack these values from params and also unpack the position and velocity from the state vector sv. As before, line 32 returns the first derivatives of x and v, which will be used in odeint() to solve the differential equation.
Lines 36-47 defines a loss function, which is a measure of the goodness of the fit of the data to the solution of the differential equation. Within this function we define the initial condition of the state variables sv0, and generate a sampled time space. Note this will be the time array which starts out at tt[0] and ends at tt[-1]. Remember an index with a minus sign counts from the end of the numpy array.Thus, tt[-1] is the last element in the array. The length of the array is len(tt)
Line 42 At each sampled time, we use odeint(sim, sv0, t, args=(params,)) to compute the state variable sv at each time in tt. Recall that we read in data for the displacement into the array xx.
Line 42 Here we sum the squares of the deviation of the recorded data and the output of the simulated system $(xx[i]-sv[i,0])^2$. For each set of trial params, we return the loss from this function
Line 49 we start with an initial guess for the parameters as params0 = np.array([1,1]).
Line 50 Finds the minimum of the loss_function, with starting values of the params0 and passing the data from the file args=(tt,xx).
The remainder is plotting the results
In generating the data for this problem I used Ex 2.4.3 and sammpled the displacement and added a random variation to the displacement data. The actual values are $c_1$=.2 and $c_2$=1.
# Ex 2.4.11
import matplotlib.pyplot as plt
import numpy as np
import csv
import scipy.optimize
from scipy.integrate import odeint
# read experimental data into lists tt and xx
tt = []
xx = []
with open("py2.4images/ex2.4.11-data.csv") as file:
reader = csv.reader(file, delimiter=',')
for row in reader:
tt.append(float(row[0]))
xx.append(float(row[1]))
# define the differential equations
def sim(sv, t, params):
x = sv[0]
v = sv[1]
c1 = params[0]
c2 = params[1]
dxdt=v
dvdt=-c1*v-c2*x
return([dxdt, dvdt])
# define the loss function
def loss_function(params, tt,xx):
sv0 = [1.0, 0.0]
t = np.linspace(tt[0], tt[-1], num=len(tt))
sv = odeint(sim, sv0, t, args=(params,))
loss = 0
for i in range(len(tt)): loss += (xx[i]-sv[i,0])**2
return(loss)
params0 = np.array([1,1])
result = scipy.optimize.minimize(loss_function, params0, args=(tt,xx))
params=(result.x[0],result.x[1])
print('c1=',params[0],'\nc2=',params[1])
plt.scatter(tt,xx)
y0 = [1.0, 0.0]
t = np.linspace(tt[0], tt[-1], num=100)
output = odeint(sim, y0, t, args=(params,))
d=output[:,0]
plt.plot(t,d, color="r")
plt.xlabel('time')
plt.ylabel('displacement')
plt.show()
