SymPy: Polynomials, Solvers, and Limits

last updated:5 JUN 2023
D. Falkenburg

Common elements of each code segment

  • import sympy: as smp imports the sympy package
  • import numpy:NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays. This is not used in many of the examples.
  • import matplotlib.pyplot: provides an implicit, MATLAB-like, way of plotting. It also opens figures on your screen, and acts as the figure GUI manager. This is not used in many of the examples.
  • smp.init_printing() sets up the print function to produce LaTex output.

documentation for this tutorial:
https://www.youtube.com/watch?v=1yBPEPhq54M \ https://dynamics-and-control.readthedocs.io/en/latest/0_Getting_Started/Notebook%20introduction.html \ https://en.wikipedia.org/wiki/SymPy

The Paradigm for Symbolic Computing

In most computer languages we are used to variables holding data types like integers, floats, lists, etc. In symbolic computing, a variable holds a symbol. In sympy we define such symbolic variables using a construct like x=smp.symbols('x'). The variable x is assigned the symbol 'x'.

Ex 4.1.1 Explanding a Polynomial

Line 3 Implements LaTeX output

Line 4 Defines x as the symbol 'x'

Line 5 Define a fourth order polynomial Line 6 Expand and print the polynomial

In [1]:
#Ex 4.1.1 
import sympy as smp
smp.init_printing()
x=smp.symbols('x')
poly = (2*x + 3)**4
poly.expand()
Out[1]:
$\displaystyle 16 x^{4} + 96 x^{3} + 216 x^{2} + 216 x + 81$

Finding functions supported in sympy type smp.tab where tab is the tab key. Try it. After about a second you will get a scroll list of all symPy functions

In [ ]:
smp.

Ex 4.1.2 LaTeX output

Note x is defined as a symbol. Since y as a function of x, line 6 will produce a LaTex expression. Note: If you replace line 6 with print(y) the output is expressed in python code. Try it.

In [6]:
#Ex 4.1.2
import sympy as smp
x=smp.symbols('x')
y=x+3*x**2
y
Out[6]:
$\displaystyle 3 x^{2} + x$

Ex 4.1.3 Roots of an Algebraic Expression

Line 2-3 import libraries

Line 4 define x as a symbolic variable holding the symbol 'x'.

Line 5 We define a symbolic equation using smp.Eq(lhs,rhs). Here the left hand side of the equation is sin(x)-tan(x) while the right hand side is 0. Setting the left hand side to 0 gives the roots of the expression .

Line 6 smp.solve( ) has two arguements: the polynomial and the variable for which we want to solve. Solve sets the function to 0 and finds the roots.

In [2]:
# Ex 4.1.3
import sympy as smp
smp.init_printing()
x=smp.symbols('x')
eq=smp.Eq(smp.sin(x)-smp.tan(x),0)
smp.solve(eq,x)
Out[2]:
$\displaystyle \left[ 0, \ - \pi, \ \pi, \ 2 \pi\right]$

Ex 4.1.3

import sympy as smp smp.init_printing() x=smp.symbols('x') eq=smp.Eq(smp.sin(x)-smp.tan(x),0) smp.solve(eq,x)

4.1.4 Complex roots

What if we have a polynomial with complex roots. This yields the complex roots. Here line 6 will display the equation eq.

In [2]:
# Ex 4.1.4
import sympy as smp
smp.init_printing()
x=smp.symbols('x')
eq=smp.Eq(x**2+2*x+10,0)
display(eq)
smp.solve(eq,x)
$\displaystyle x^{2} + 2 x + 10 = 0$
Out[2]:
$\displaystyle \left[ -1 - 3 i, \ -1 + 3 i\right]$

4.1.5 Solving an Equation of Several Variables Symbolically for y(x,z)

Line 3 We define multiple variables as symbols in this statement. NOTE: COMMAS ON THE LEFT SIDE BUT NOT IN THE ARGUMENT of smp.symbols() Line 4 trig functions defined in sympy: smp.sin()
Note: the right hand side of this equation is NOT 0, but 10.

In [4]:
# Ex 4.1.5
import sympy as smp
x, y, z = smp.symbols('x y z')
eq=smp.Eq(x**2+y*smp.sin(z),10)
display(eq)
smp.solve(eq,y)
$\displaystyle x^{2} + y \sin{\left(z \right)} = 10$
Out[4]:
$\displaystyle \left[ \frac{10 - x^{2}}{\sin{\left(z \right)}}\right]$

4.1.6 Another Example

Note: depending on the values of x and y, there may be no solutions or multiple periodic solutions. The solution for one period of the sine are given here.

In [5]:
# Ex 4.1.6
import sympy as smp
smp.init_printing()
x, y, z = smp.symbols('x y z')
eq=smp.Eq(x**2+y*smp.sin(z),0)
smp.solve(eq,z)
Out[5]:
$\displaystyle \left[ \operatorname{asin}{\left(\frac{x^{2}}{y} \right)} + \pi, \ - \operatorname{asin}{\left(\frac{x^{2}}{y} \right)}\right]$

Ex 4.1.6a

Assign smpl.solve to a new variable soln. Since will also be type symbol. We already know that it is a list of solutions. To print the value for index 0 we simply use soln[0]

In [2]:
# Ex 4.1.6
import sympy as smp
smp.init_printing()
x, y, z = smp.symbols('x y z')
eq=smp.Eq(x**2+y*smp.sin(z),0)
soln=smp.solve(eq,z)
soln[0]
Out[2]:
$\displaystyle \operatorname{asin}{\left(\frac{x^{2}}{y} \right)} + \pi$

Ex 4.1.7 Lambdify--Converting a Sympy Expression to a Numerical Expression

"Lambdify is a function to transform SymPy expressions to lambda functions which can be used to calculate numerical values very fast." Ref

line 7In this example we will plot a graph of a function z_sols which symbolically relates z to x and y. All of these variables are symbolic variables.

Line 8 In order to make a graph we must be able to plug numbers into the exression we are plotting. That cannot be done for a symbolic variable. The SymPy function Lambdify() provides the means of doing this. Remember that a lambda function allows us to write an anonomous function in a single line. Hence the name of this method lambdify(). exprs_f is NOT a symbolic variable. lambdify([x,y],z_sols[0]) can be read: find values of z_sols[0] for numerical values of x and y.

Line 9 x_num is defined as a NumPy array thru linspace--100 points starting at 0 and ending at 1.

Line 10 y_num is defined as a single number 2.

Line 11 is uses plt.plot to plot exprs_f(x_num,y_num) vs. x_num

experiment

Define y using linspace over the range from -2 to +2 using 200 points. Plot the surface plot for the function.

In [13]:
#Ex 4.1.7
import sympy as smp
import numpy as np
import matplotlib.pyplot as plt
x, y, z = smp.symbols('x y z')
eq=smp.Eq(z**2-x**3-y,4)
z_sols=smp.solve(eq,z)
display(z_sols)
f1=smp.lambdify([x,y],z_sols[0])
f2=smp.lambdify([x,y],z_sols[1])
x_num=np.linspace(0,16,100)
y_num=2
plt.xlabel('x')
plt.ylabel('z')
plt.plot(x_num,f1(x_num,y_num))
plt.plot(x_num,f2(x_num,y_num))
plt.show()
$\displaystyle \left[ - \sqrt{x^{3} + y + 4}, \ \sqrt{x^{3} + y + 4}\right]$

Ex 4.1.8 Solving Multiple Equations

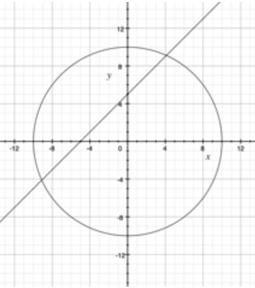Let's begin with finding the solution of the following equations: $$ y=mx+b \\ z=x^2+y^2 $$ Line 5-6 We first create two equation objects

eq1=smp.Eq(y-x,5) eq2=smp.Eq(x2+y2,100)

Line 7 creates the solution for the pair [x,y]. As expected there are two sets of [x,y] that satisfy the equations.

Note: if b is too large, there will be no real solution.

In [3]:
# Ex 4.1.8
import sympy as smp
smp.init_printing()
x, y, z, = smp.symbols('x y z')
eq1=smp.Eq(y-x,5)
eq2=smp.Eq(x**2+y**2,100)
smp.solve([eq1,eq2],[x,y])
Out[3]:
$\displaystyle \left[ \left( - \frac{5}{2} + \frac{5 \sqrt{7}}{2}, \ \frac{5}{2} + \frac{5 \sqrt{7}}{2}\right), \ \left( - \frac{5 \sqrt{7}}{2} - \frac{5}{2}, \ \frac{5}{2} - \frac{5 \sqrt{7}}{2}\right)\right]$

4.1.8a Changing Parameters in the Last Problem

In this example we have changed b from 5 to 25. The solution yields complex numbers.

In [7]:
#Ex 4.1.8a
import sympy as smp
import numpy as np
import matplotlib.pyplot as plt
smp.init_printing()
x, y, z, = smp.symbols('x y z')
eq1=smp.Eq(y-x,25)
eq2=smp.Eq(x**2+y**2,100)
smp.solve([eq1,eq2],[x,y])
Out[7]:
$\displaystyle \left[ \left( - \frac{25}{2} - \frac{5 \sqrt{17} i}{2}, \ \frac{25}{2} - \frac{5 \sqrt{17} i}{2}\right), \ \left( - \frac{25}{2} + \frac{5 \sqrt{17} i}{2}, \ \frac{25}{2} + \frac{5 \sqrt{17} i}{2}\right)\right]$

4.1.8b Constraining the Solution Space

Line 6 In the preceeding example we change the definition of the symbols to include the constraint that they be real. The solution list is null.

In [8]:
# EX 4.1.8b
import sympy as smp
import numpy as np
import matplotlib.pyplot as plt
smp.init_printing()
x, y, z, = smp.symbols('x y z', real=True)
eq1=smp.Eq(y-x,25)
eq2=smp.Eq(x**2+y**2,100)
smp.solve([eq1,eq2],[x,y])
Out[8]:
$\displaystyle \left[ \right]$

4.1.8c Using nsolve( ) Solving for a Numerical Solution to 4.1.8

For the examples above, we used solve() to find a symbolic solution. There is another function nsolve() which produces a numerical solution. Going back to Ex 4.1.8, lets try to get a numerical answer. Here we use the method .nsolve(), which has an additional arguement-- an initial guess at the solution. Recall in this case, the solution is an x,y pair. Notice that nsolve returns only ONE of the two solutions. If we seed nsolve with [-2,-2] we will get the other solution. Lines 2-8 are identical to Ex 4.1.8 Line 9 looks the same except that smp.solve() is replaced by smp.nsolve().

NOTE The ' ' surrounds the group of symbols it is ('x y z') NOT ('x' 'y' 'z')

In [11]:
# Ex 4.1.8c
import sympy as smp
import numpy as np
import matplotlib.pyplot as plt
smp.init_printing()
x, y, z, = smp.symbols('x y z')
eq1=smp.Eq(y-x,5)
eq2=smp.Eq(x**2+y**2,100)
smp.nsolve([eq1,eq2],[x,y],[2,2])
Out[11]:
$\displaystyle \left[\begin{matrix}4.11437827766148\\9.11437827766148\end{matrix}\right]$

Ex 4.1.9 Limits

Suppose we want to find
$$\lim_{x \to \pi} \sin(x/2+\sin(x))$$
Line 5 We use smp.limit(f,x,value). Were f is some function of x, and we want to find the limit as x approaches value, in this case $\pi$ . Don't forget trig function must be smp. if they are to be treated as symbols.

In [ ]:
# Ex 4.1.9 
import sympy as smp
smp.init_printing()
x=smp.symbols('x')
smp.limit(smp.sin(x/2+smp.sin(x)),x,smp.pi)

4.1.10 Indeterminate Forms

SymPy can handle indeterminate forms. Consider: $$\lim_{x \to 0} \frac{x}{\sin(x)}$$

In [15]:
# Ex 4.1.10
import sympy as smp
smp.init_printing()
x=smp.symbols('x')
smp.limit(x/(smp.sin(x)),x,0)
Out[15]:
$\displaystyle 1$
In [ ]: